Aiming to most difficult problems in symbolic computation, we first propose the idea of “obtaining exact value by approximate computations”. Based on the idea, we design a symbolic-numeric algorithm for polynomial factorization, which corrects a mistake made by Sasaki, who is a famous scholar in symbolic computation. We have developed a family of efficient symbolic-numeric algorithms for computing the real solutions of polynomial systems. Some of them have been implemented in the RegularChains library of Maple awarded “the best software" of ACM ISSAC.

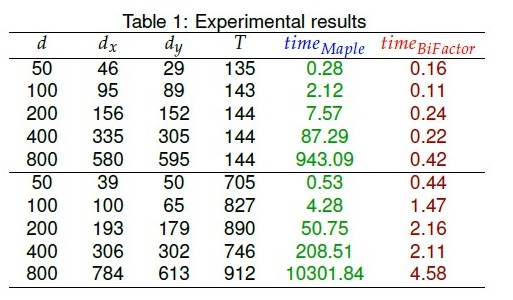
Comparing with Maple, one of the most famous computer algebra system around the world, our algorithm only needs 1/1000, or less, time that Maple uses to factor the same polynomial with appropriate size; see Table 1 for comparison data.

Moreover, the algorithm is able to factorize such polynomials with extremely high degrees, e.g., polynomials with total degree 10000000, that the built-in function factor does not apply.

Polynomial factorization has many applications in various fields including the simplification, primary decomposition, solving polynomial equations, algebraic coding theory, cryptography, stability analysis of biological system, program verification, control and optimization, etc.